Page 169 - EI2019.pdf

2.8 Cota inferior de Cram´ er-Rao 161

Por lo tanto, todo estimador insesgado para θ yconstruidoa partirde una
muestra aleatoria de tama˜no n en la distribuci´on exponencial tiene varianza

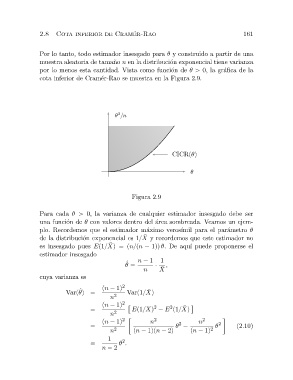
por lo menos esta cantidad. Vista como funci´on de θ ą 0, la gr´afica de la
cota inferior de Cram´er-Rao se muestra en la Figura 2.9.

2
θ {n

CICRpθq

θ

Figura 2.9

Para cada θ ą 0, la varianza de cualquier estimador insesgado debe ser
una funci´on de θ con valores dentro del ´area sombreada. Veamos un ejem-
plo. Recordemos que el estimador m´aximo veros´ımil para el par´ametro θ
¯
de la distribuci´on exponencial es 1{X yrecordemos queesteestimador no
¯
es insesgado pues Ep1{Xq“pn{pn ´ 1qq θ. De aqu´ıpuede proponerse el
estimador insesgado
ˆ n ´ 1 1
θ “ ¨ ¯ ,
n X
cuya varianza es

2
ˆ pn ´ 1q ¯
Varpθq“ Varp1{Xq
n 2
2
pn ´ 1q “ ¯ 2 2 ¯ ‰
“ Ep1{Xq ´ E p1{Xq
n 2
2 „ 2 2 
pn ´ 1q n 2 n 2
“ θ ´ θ (2.10)
n 2 pn ´ 1qpn ´ 2q pn ´ 1q 2
1
2
“ θ .
n ´ 2