Page 73 - cepe2012.pdf

i i

“cepeMathBookFC” — 2012/12/11 — 19:57 — page 63 — #67
i i

8. DISTRIBUCIONES DE PROBABILIDAD 63

f .x/ f .x/
D 5
D 4
D 3 n D 5
1/2 1/2 n D 7
n D 10

x x
1 2 3 4 5 6 1 2 3 4 5 6
(b) D 3
(a) n D 5

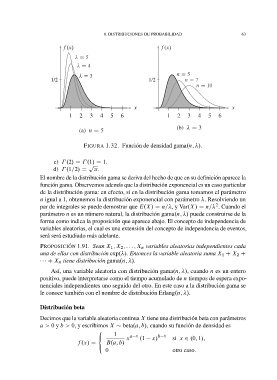
FIGURA 1.32. Funci´ on de densidad gama.n; /.

c) .2/ D .1/ D 1.
p
d) .1=2/ D .
El nombre de la distribuci´ on gama se deriva del hecho de que en su definici´ on aparece la
funci´ on gama. Observemos adem´ as que la distribuci´ on exponencial es un caso particular
de la distribuci´ on gama: en efecto, si en la distribuci´ on gama tomamos el par´ ametro
n igual a 1, obtenemos la distribuci´ on exponencial con par´ ametro . Resolviendo un
2
par de integrales se puede demostrar que E.X/ D n=, y Var.X/ D n= . Cuando el
par´ ametro n es un n´ umero natural, la distribuci´ on gama.n; / puede construirse de la
forma como indica la proposici´ on que aparece abajo. El concepto de independencia de
variables aleatorias, el cual es una extensi´ on del concepto de independencia de eventos,
ser´ a ser´ a estudiado m´ as adelante.
PROPOSICI ´ ON 1.91. Sean X 1 ; X 2 ; : : : ; X n variables aleatorias independientes cada
una de ellas con distribuci´ on exp./. Entonces la variable aleatoria suma X 1 C X 2 C
C X n tiene distribuci´ on gama.n; /.
As´ ı, una variable aleatoria con distribuci´ on gama.n; /, cuando n es un entero
positivo, puede interpretarse como el tiempo acumulado de n tiempos de espera expo-
nenciales independientes uno seguido del otro. En este caso a la distribuci´ on gama se
le conoce tambi´ en con el nombre de distribuci´ on Erlang.n; /.

Distribuci´ on beta
Decimos que la variable aleatoria continua X tiene una distribuci´ on beta con par´ ametros
a > 0 y b > 0, y escribimos X beta.a; b/, cuando su funci´ on de densidad es
1
8
x .1 x/ si x 2 .0; 1/;
< a 1 b 1
f .x/ D B.a; b/
0 otro caso.
:

i i

i i