El signo ![]() usaremos para indicar la aproximación en el sentido de cuadrados
mínimos, esto es, se minimiza la norma del residual r = Ax
- b, en otras palabras, hemos de minimizar el residual
usaremos para indicar la aproximación en el sentido de cuadrados
mínimos, esto es, se minimiza la norma del residual r = Ax
- b, en otras palabras, hemos de minimizar el residual
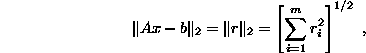
En forma equivalente, si consideramos la función cuadrática
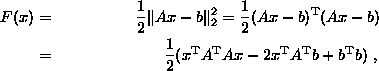
la cual es una función diferenciable en x. Una condición necesaria para el mínimo de F(x) es que el vector gradiente sea cero, es decir:
![]()
Lo que nos conduce a un sistema de ecuacnines llamadas ecuaciones normales, las cuales son escritas:
![]()
La solución al sistema ![]() es usualmente calculada por el siguiente algoritmo:
es usualmente calculada por el siguiente algoritmo:
La matriz ![]() es simétrica y es definida positiva y entonces podemos emplear la
factorización de Cholesky
es simétrica y es definida positiva y entonces podemos emplear la
factorización de Cholesky![]() para primero resover
para primero resover ![]() y finalmente calcular x en la forma
y finalmente calcular x en la forma ![]() .
.
Desafortunadamente ![]() es siempre una matriz mal-condiciona y su infuencia en la propagación
de los errores es terrible.
es siempre una matriz mal-condiciona y su infuencia en la propagación
de los errores es terrible.
Existen métodos que no calculan ![]() y
resuelven
y
resuelven ![]() en
forma directa usando la descomposición QR
o bién tratando el problema original como un problema de minimización.
en
forma directa usando la descomposición QR
o bién tratando el problema original como un problema de minimización.