En muchas aplicaciones estamos interesados en describir el comportamiento
de un conjunto de datos para entonces poder predecir su comportamiento
hacia el interior del conjunto.
Si ![]() es un polinomio de grado
n-1,
este se encuentra en el espacio generado por
es un polinomio de grado
n-1,
este se encuentra en el espacio generado por ![]() ,
esto es
,
esto es
![]()
y entonces existe una única combinación lineal tal que
![]()
Ahora bien, ![]() es el polinomio
de grado n-1 que resuelve el problema de interpolación
es el polinomio
de grado n-1 que resuelve el problema de interpolación
![]()
entonces tendremos un conjunto de ecuaciones lineales
![]()
un sistema de n ecuaciones lineales, el cual puede ser expresado en forma matricial como
Ac=y
donde A es la matriz de Vandermonde
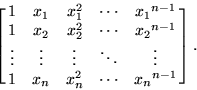
c es el vector de coeficientes y y las ordenadas de los
puntos.
La matriz de Vandermonde es no singular y no requiere pivoteo, siempre
que los puntos Xi se encuentren ordenados.
Por otra parte la mtriz de Vandermonde es una matriz muy mal condicionada.
El problema de interpolación polinomial es un problema mal condicionado,
experimente con el programa en java
Interpolación
con polinomios y con splines para observar el comportamiento de la
interpolación polinomial.
Pero no siempre estamos interesados en obtener el polinomio que pase por los puntos. En ocasiones nos interesa saber el comportamiento de los dato o estimar ese comportamiento atravéz del comportamiento de las funciones polinomiales.
Si nuestros datos siguen una tendencia y consideramos puede ser aproximada por un polinomio de grado menor, mucho menor que el número de datos, podemos intentar aproximar el residual de la aproximación del modelo polinomial por un problema de mínimos cuadrados y obtener las Ecuaciones Normales asociadas. Esto lo podemos extender a modelos no lineales.