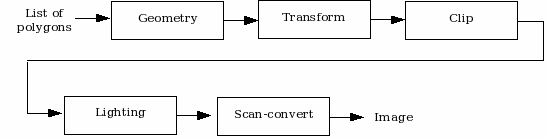
Figure 1. A 3D rendering pipeline.
The
Parallel Pipes and Filters Pattern
A Functional Parallelism Architectural Pattern for Parallel Programming
Jorge L. Ortega-Arjona
Departamento de Matemáticas
Facultad de Ciencias, UNAM
Abstract
The Parallel Pipes and Filters pattern is an architectural pattern for parallel programming, used when a problem can be understood in terms of functional parallelism. It is an extension with aspects of parallelism of the original Pipes and Filters pattern presented in the Pattern-Oriented Software Architecture book, by Buschmann, Meunier, Rohnert, Sommerland, and Stal. The Parallel Pipes and Filters pattern proposes a solution in which different operations are actually simultaneously performed on different ordered pieces of data, that “flow” through the operations. Operations carried out by each component depend only on the availability of results from preceding components.
1. Introduction
Parallel processing is the division of a problem, described as data and an algorithm, among multiple processing components that operate simultaneously. The expected result is a more efficient completion of the solution to the problem. The main advantage of parallel processing is its ability to handle tasks of a scale that would be unrealistic or not cost-effective for other systems [CG88, Fos94, ST96, Pan96, OR98, And00]. The power of parallelism centres on partitioning a big problem in order to deal with complexity. Partitioning is necessary to divide such a big problem into smaller sub-problems that are more easily understood, and may be worked on separately, on a more “comfortable” level. Partitioning is especially important for parallel processing, because it enables software components to be not only created separately but also executed simultaneously.
Requirements of order of data and operations dictate the way in which a parallel computation has to be performed, and therefore, impact on the parallel software design [OR98]. Depending on how the order and dependence of both, data and operations, are present in the problem description, it is possible to consider that most parallel applications fall into one of three forms of parallelism: domain parallelism, activity parallelism, and functional parallelism [OR98]. Examples of each form of parallelism are the Communicating Sequential Elements pattern [OR00], as an example of domain parallelism; the Shared Resource pattern [OR03], as an instance of activity parallelism; and the Parallel Pipes and Filters pattern, representing functional parallelism.
The pipes and filters (or pipeline) structure has been commonly used and described in parallel programming by many authors [CT92, NHST94, Fos94, KSS96, HPCN98, And00]. Moreover, it has been previously presented or referred to in a pattern form by several other authors [VBT95, POSA96, Lea96, OR98, MSM04]. Nevertheless, the objective of the present paper is to search for a pattern description for the Parallel Pipes and Filters which focuses on the particular characteristics of a parallel programming context and the description of its problem in terms of a division of the algorithm and the data to be operated on. The main idea is to discuss about the characteristics of both, problem and context, aiming to find the reasons for using the Parallel Pipes and Filters as a feasible solution in terms of a flow organisation of parallel communicating software components. The objective is to help the parallel programmer when considering the development of a solution based on the Parallel Pipes and Filters pattern, providing a selection criteria in the context of parallel programming.
2. The Parallel Pipes and Filters Pattern
The Parallel Pipes and Filters pattern presented here extends the original Pipes and Filters pattern [POSA96, Shaw95, SG96] with aspects of functional parallelism. Each parallel component simultaneously performs a different step of the computation, following a precise order of operations on ordered data that is passed from one computation stage to another, as a flow through the whole structure [OR98].
Functional parallelism is the form of parallelism that involves problems where a computation can be described in terms of a series of simultaneous time-step ordered operations, on a series of ordered values or data, with predictable organization and interdependencies. As each step represents a change of the input for value or effect over time, a high amount of communication between components in the solution (in the form of a flow) should be considered. Conceptually, a single data value or transformation is performed repeatedly [CG88, Fos94, Pan96, OR98].
Example: Graphics Rendering
In image processing, graphics rendering is a jargon phrase that has come to mean “the collection of operations necessary to project a view of an object or a scene onto a view surface”. In common applications for the film and video industry, rendering a special effect scene of 10 seconds using a standard resolution of 2048´1536 pixels takes up to 130 hours of processing time, using the C programming language on a single high-end Macintosh or PC platform [HPCN98].
The input to a polygonal renderer is a geometry, presented as a list of polygons, and the output is an image, in which a colour for each pixel on the screen is obtained. The problem, hence, is to transform the list of polygons into an image. For example, in order to build up a 3D scene, five general tasks are considered to be performed (Figure 1) [KSS96]. Such stages are specialised in order to (a) enumerate the objects in the scene and generate geometric descriptions of each one; (b) apply a coordinate transformation to the geometry to account for the camera's viewing position, direction, and focal length; (c) clip the geometry so that elements outside the field of view of the camera are excluded; (d) apply a lighting model to compute a shade for each of the objects; and (e) scan-convert each face of the objects, drawing the faces in a frame buffer to obtain the final raster image. Hence, creating shaded renderings of 3D geometric objects can be described as a series of independent processing stages on ordered data.
The time required to render a scene usually can be decreased using a parallel pipes and filters approach. We can potentially carry out this computation more efficiently by overlapping each one of the tasks in time:
Each component is able to independently process different pieces of data through time until completion, so each component represents a processing unit or stage, which can potentially execute simultaneously with the rest of components, and
Allowing a simultaneous flow of data from one stage to the next, receiving ordered data from the previous stage and sending results to the next one.
Using a parallel approach, with a 16 node CYCORE (a Parsytec parallel machine) programmed in C, this process is reduced to 10.5 hours [HPCN98].

Figure 1. A 3D rendering pipeline.
Notice that this example is composed of heterogeneous stages, where each stage performs a different kind of activity, producing different types of data between stages. Moreover, the number of stages is fixed by the problem description, and cannot necessarily be increased. To make matters still worse, the different activities carried out by each stage are likely to require different amounts of time, so if each stage is considered to be executed in parallel, the result will not be balanced: one stage will be the bottleneck, and others will be partially idle. Thus, it is very helpful to gauge at the outset the amount of work that each stage will do.
A contrasting approach is composed of homogeneous stages, where each stage carries out the same activity. In effect, the pipes and filters structure of n stages divides the work into n pieces. This situation seems to relief some of the difficulties of the heterogeneous pipeline, but still, synchronisation between stages is a difficult problem to deal with.
Notice that often it is needed to think carefully about the problem to view the decomposition of the algorithm as potentially simultaneous activities. Occasionally, it is required to completely re-state the problem, or to re-structure how it is described, in order to obtain a suitable solution.
Context
Start the design
of a coordination organisation of a parallel system, using a specific
programming language for a particular parallel hardware. Consider
the following contextual assumptions:
The parallel platform and programming environment to be used are known, offering a reasonably level of parallelism in terms of number of processors or parallel cycles available. For the Graphics Rendering example, a parallel solution is proposed to be executed using a given 16 node CYCORE parallel computer.
The programming language to be used, based on a certain paradigm, is determined, and a compiler is commonly available for the parallel platform. Today, many programming languages have parallel extensions for many parallel platforms [Pan96], as it is the case of C, which can be extended for a particular parallel computer or use libraries (like PVM or MPI) to achieve process communication.
The problem to solve, expressed as an algorithm and data, is found to be an open ended one, that is, involving tasks of a scale that would be unrealistic or not cost-effective for other systems to handle. Consider the Graphics Rendering example: a common applications for the film industry to render a special effect scene of 10 seconds requires 130 hours of processing time on a single high-end Macintosh or PC platform. A complete feature film, or even a short film, would require several thousands hours only for rendering each scene.
The main objective is how to execute the task in the most time-efficient way. In the Graphics Rendering problem, the time is reduced from 130 hours to 10.5 hours.
Problem
An algorithm, composed of ordered and independent computations, is required to operate on regular and ordered data. The computations are ordered but independent from each other, in the sense that, if data is available, each computation can be carried out until completion without interference (so there is an opportunity to overlap successive computations). If the computations were carried out serially, the output data set of the first operation would serve as input to the operations during the next step, whose output would in turn serve as input to the subsequent step-operations. Hence, the focus of the problem analysis should be on a potential division of the algorithm into independent computations, which have to be executed in the order prescribed by the algorithm itself.
On the other hand, the data is regular and ordered, meaning that, at first, it may not be properly considered for division. The only criteria for data division is driven by the independence between successive computations: there should be an adequate amount of data available for each computation so each computation can be carried out without interference. Moreover, notice that along the whole set of computations, data can be transformed, even producing new data of a different type. Hence, the amount of data passed from one computation to the next also may have influence on the whole processing, as a group of simultaneous computations.
For instance, consider the Graphics Rendering example: for each polygon of the list, it is required to (a) generate its geometric description, (b) apply a transformation to account for the camera, (c) clip the geometry, (d) shade, and (e) scan-convert, drawing the faces to obtain the final image. When this rendering process is executed serially, it requires that all data is processed in a particular stage before the following stage starts processing. Notice as well that the data input of each stage is used to produce a different type of output data, which is passed to the next stage throughout the rendering process.
Forces
Considering the problem description and granularity and load balance as other elements of parallel design [Fos94, CT92] the following forces should be considered:
Maintain the precise order of computations. Such an order represent the very algorithm to be applied to each piece of data. For example, in the Graphics Rendering example, it is important to control the order of where and when data is operated, by allowing it to “flow” through each rendering stage. This allows obtaining the effect of operation overlapping through time.
Preserve the order of data among all operations. The result of the whole computation is the effect of applying each algorithm step on each piece of data, so the order of data is a basic feature that should be preserved for obtaining ordered results. In the Graphics Rendering example, each stage receives data from the previous stage, processes it, and produces more data that serves as input to the next stage. Nevertheless, data must be operated in a strict order, so the result of the whole computation is orderly obtained.
Consider the independence among step-operations, which potentially can be carried out processing different pieces of data. In the Graphics Rendering example, each rendering stage performs autonomously a different computation on different pieces of data. The objective is to obtain the best possible benefit from a functional parallelism.
Distribute process into regular amounts among all step-operation. In the Graphics Rendering example, a different operation must be performed on each stage to obtain data to be processed at the next stage. All data is incrementally and simultaneously operated on. Nevertheless, if one stage takes more time than the others, it would represent a bottleneck for the flowing data.
Improvement in performance is achieved when execution time decreases. Our main objective is to carry out the computation in the most time-efficient way.
Solution
Introduce parallelism by allowing the overlap through time of the ordered but independent computations. The operations represent each stage of the whole computation, as incrementally ordered steps which are simultaneously executed. Data from different steps are used to generate change of the input over time. Conceptually, a single data object is transformed. The first set of components begins to compute as soon as the first data are available, during the first time-step. When its computation is finished, the result data is passed to another set of components in the second time-step, following the order of the algorithm. Then, while this computation takes place on the data, the first set of components is free to accept more new data. The results from the second time-step components can also be passed forward, to be operated on by a set of components in a third-step, while now the first time-step can accept more new data, and the second time-step operates on the second group of data, and so forth [POSA96, CG88, Shaw95, Pan96].
Structure
This pattern is called “Parallel Pipes and Filters” since data is passed as a flow from one component (representing a computation stage) to another along a pipeline of different simultaneous processing components. The key feature is that data results are passed just one way through the structure. The complete parallel execution incrementally builds up, when data becomes available at each stage. Different components simultaneously exist and process during the execution time (Figure 2).
Participants
Filter. The responsibilities of a filter component are to get input data from a pipe, to perform an operation on its local data, and to send output result data to one or several pipes. In the Graphics Rendering example, each time step a parallel filter is expected to receive data from the previous filter (through an input pipe), perform a step of the actual rendering, and send partial results to the next filter (through another output pipe).
Pipe. The responsibilities of a pipe component are to transfer data between filters, sometimes to buffer data or to synchronise activity between neighbouring filters. In order to synchronise the activities, pipe components should take into consideration the amount of data that has to be communicated from one filter to the next one, so both their operations do not conflict with each other. In the Graphics Rendering problem, pipes are expected to handle the communication and synchronisation of data values between neighbouring stages, giving the impression of a flow through the processing structure.
Source. The responsibility of a source component is to provide initial data to the first filter. In the Graphics Rendering example, this may be simply to open a file containing the list of polygons to be rendered, and provide it to the “Geometry” stage.
Sink. The responsibility of a sink component is to get and gather the final result of the whole computation. In the Graphics Rendering problem, this means to preserve the data of the image produced, perhaps saving it into a file after the “Scan-convert” stage.
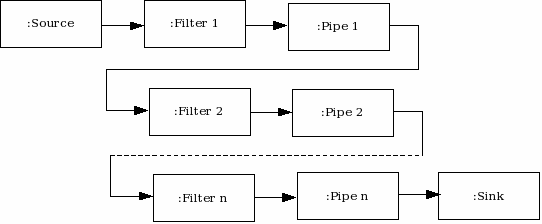
Figure 2. Object Diagram of the Pipes and Filters pattern.
Dynamics
Due to the parallel execution of the components of the pattern, the following typical scenario is proposed to describe its basic run-time behaviour. As all filters and pipes are active simultaneously, they accept data, operate on it in the case of filters, and send it to the next step. Pipes synchronise the activity between filters. This approach is based on the dynamic behaviour exposed by the Pipes and Filters pattern in [POSA96], adding the simultaneous execution of software components that parallel programming allows.
In this simple scenario, the operation of the source and sink components are avoided, in order to stress the overlapping through time of the following general steps (figure 3):
Pipe A receives data from a Data Source or another previous filter, synchronising and transferring it to the Filter N.
Filter N receives the package of data, performs operation Op.n on it, and delivers the results to Pipe B. At the same time, new data arrives to the Pipe A, which delivers it as soon as it can synchronise with Filter N. Pipe B synchronises and transfers the data to Filter M.
Filter M receives the data, performs Op.m on it, and delivers it to Pipe C, which sends it to the next filter or Data Sink. Simultaneously, Filter N has received the new data, performed Op.n on it, and synchronising with Pipe B to deliver it.
The previous steps are repeated over and over until no further data is received from the previous Data Source or filter.
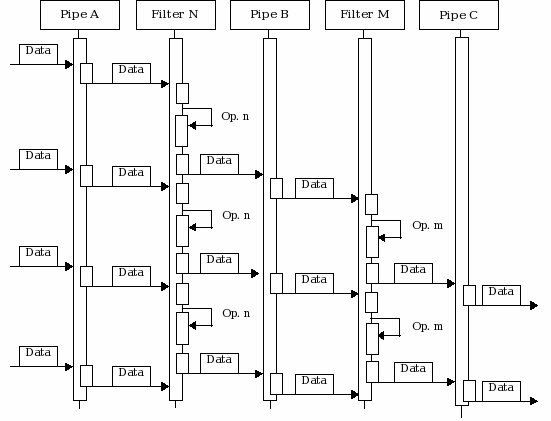
Figure 3. Interaction Diagram of the Pipes and Filters pattern.
Implementation
An architectural exploratory approach to design is described below, in which hardware-independent features are considered early, and hardware-specific issues are delayed in the implementation process. This method structures the implementation process of parallel software based on four stages [Fops94, OR98]. During the first two stages, attention is focused on concurrency and scalability characteristics. In the last two stages, attention is aimed to shift locality and other performance-related issues. Nevertheless, it is preferred to present each stage as general considerations for design instead of providing details about precise implementation. These implementation details are pointed more precisely in the form of references to design patterns for concurrent, parallel, and distributed systems of several other authors [Sch95, Sch98a, Sch98b, POSA00].
Partitioning. The computation that is to be performed is decomposed, attending the ordered operations to be performed into a sequence of different operation stages, in which orderly data is received, operated on and passed to the next stage. Attention focuses on recognising opportunities for simultaneous execution between subsequent operations, to assign and define potential filter components. Initially, filter components are defined by gathering operation stages, considering characteristics of granularity and load-balance. As each stage represents a transformational relation between input/output data, filters can be composed of a single processing element (for instance, a process, task, function, object, etc.) or a subsystem of processing elements. Design patterns [GHJV95, POSA96, PLoP94, PLoP95] can be useful to implement the latter ones; particularly, consider the Active Object pattern [LS95, POSA00] and the "Ubiquitous Agent" pattern [JP96].
Communication. The communication required to coordinate the simultaneous execution of stages is determined, considering communication structures and procedures to define the pipe components. Common characteristics that should be carefully considered are the type and size of the data to be passed, and the synchronous or asynchronous coordination schema, trying to reduce the costs of communication and synchronisation. Usually, a synchronous coordination is commonly used. The implementation of pipe components obeys to features of the programming language used. If the programming language has defined the necessary communication structures for the size and type of the data, a pipe in general can be usually defined in terms of a single communicating element (for instance, a process, a stream, a channel, etc.). However, in case that more complexity in data size and type is required, a pipe component can be implemented as a subsystem of elements, using design patterns. Especially, patterns like the Broker pattern [POSA96] and the Composite Messages pattern [SC95].
Agglomeration. The filter and pipe structures defined in the previous stages should be evaluated with respect to the performance requirements and implementation costs. Once initial filters are defined, pipes are considered simply to allow data flow between filters. If an initial proposed agglomeration does not accomplish the expected performance, the conjecture-test approach can be used to propose another agglomeration schema. Recombining the operations by replacing pipes between them modifies the granularity and load balance, aiming to balance the workload and to reduce communication costs.
Mapping. Each component is assigned to a processor, attempting to maximise processor utilisation and minimise communication costs. Usually, mapping is specified as static. As a "rule of thumb", these systems may have a good performance when implemented using shared-memory machines, or can be adapted to distributed-memory systems, if the communication network is fast enough to pipe data sets from one filter to the next [Pan96].
Example Resolved
The Parallel Pipes an Filters pattern can be used in a parallel program that computes a rendering of a scene from a geometric description. The program structure can take several forms, depending on many factors, including the choice of rendering algorithm. The example here presents five stages [KSS96], as outlined below. Typed tokens are passed down. For example, a polygon is one kind of token passed down the entire length of the pipes and filters structure, with an attached data structure defining the geometry and colour of the polygon.
Partitioning
The Parallel Pipes and Filters pattern is used to obtain a Software Structure that deals with the Graphics Rendering problem, describing the actual processing as a cooperation between different sequential filters, which simultaneously perform calculations and communicate partial results through pipes with their neighbours. The main stages of the Software Structure follow the steps of the algorithm already described. So, the filter stages in which the rendering computation is divided are [KSS96]:
GEN. The first stage of the pipeline is really the main function, which determines the viewing parameters of the scene, generates the geometric descriptions of objects, and so on. These functions call a few routines in the graphics package to compute a rendering. In our example, the graphics package controls the pipeline structure, which is hidden from the client.
TRAN. The second stage of the pipe performs geometric transformations. For example, each vertex of a polygon is transformed first into a camera coordinate system to position the polygon relative to the camera and then into a perspective coordinate system, which accounts for the perspective projection of the camera.
CLIP. The third stage clips polygons to the limits of the viewing region of the camera. Polygons or portions of polygons that lie outside the field of view or behind the camera are rejected.
EDGE. The fourth stage computes a colour, or shade, appropriate for each vertex of the polygon. This computation requires knowing the colour and surface properties assigned to the polygon, the normal vector at the vertex, and details of lights specified for the scene. This stage also builds an edge data structure and attaches it to the polygon token.
PIXEL. The final stage executes a scan-line algorithm to enumerate the pixels covered by the polygon and to compute the depth and colour of the polygon at each pixel. At each pixel, the depth is compared to the depth recorded in a z-buffer, to determine whether the polygon's pixel is closer to the camera than whatever other object has been previously recorded in the z-buffer, and if so, the polygon's colour and depth replace those of the other polygon. In simplified form, the algorithm within this stage is:
for (y = top of polygon; y > = bottom of the polygon; y--) {
for (each pair of polygon edges crossing scan-line y) {
for (x = left edge; x < = right edge; x++) {
if (z > = z_buffer[x,y]) {
z_buffer[x,y] = z;
image[x,y] = polygon_colour;
}
}
}
}
Communication
Communication between filters, as stages within the Graphics Rendering algorithm, is carried out by allowing data to flow down the pipes, in the form of tokens [KSS96]. Thus, in order to maintain proper synchronisation, the state held by a filter is changed only as a consequence of processing a token in such a filter. This strategy avoids any data locking, save for that embodied in the pipes between filters: filters refer only to data that they “own”. For example, the routine in the graphics package responsible for initialisation sends a begin token down the whole structure. This token specifies the width and height of the output image, in pixels. Each filter that needs to know this information copies these two parameters into static variables accessible only to that filter. Of course, the begin token also affords each filter the opportunity to do any initialisation required. As another example, the light token is sent down with information about a light used to illuminate the scene; this information is captured in the EDGE filter.
Not all tokens flow down the full length of the pipeline structure. Of course, tokens such as the begin, end, and polygon proceed through all filters. Each filter that processes one of these tokens is responsible for forwarding the token onward by putting it on its output pipe, which sends it to the next filter. However, the transformation token, used to update the current transformation held in the TRAN filter, need to flow only as fas as the TRAN filter. After the token is processed, the filter simply returns the token to the free storage rather than placing it on its output pipe.
The token flow is also data-dependent. The polygon token is abandoned if a filter determines that the polygon described by a token need not to be communicated further. There are two cases: (a) back-face culling, if the TRAN filter determines that the polygon faces away from the camera; and (b) clipping, if the CLIP filter determines that no part of the polygon falls within the viewing region.
Agglomeration and Mapping
The uneven processing duties of the filters at different stages of the computation, coupled with the potential for early rejection of polygons, make it difficult to balance the pipeline structure. In most cases, the PIXEL filter will require the most computation. Indeed, to balance the processor utilisation, it may be necessary to further divide the PIXEL filter, for example by splitting the main loop illustrated above, so that several threads can compute concurrently. Such a hybrid approach is often found in parallel application, combining several algorithm paradigms.
Known uses
The butterfly communication structure, used in many parallel systems to obtain the Fast Fourier Transform (FFT), presents a basic Parallel Pipes and Filters pattern. Input values are propagated through intermediate stages, where filters perform calculations on data when it is available. The whole computation can be viewed as a flow through crossing pipes that connect filters [Fos94].
Parallel search algorithms mainly present a pipes and filters structure. An example is the parallel implementation of the CYK Algorithm (Cocke, Younger and Kasami), used to answer the membership question: "Given a string and a grammar, is the string member of the language generated by the grammar?" [CG88, NHST94].
Operations for image processing, like convolution, where two images are passed as streams of data through several filters (FFT, multiplication and inverse FFT) in order to calculate their convolution [Fos94].
Video decompression. A three-stage pipes and filters organisation is used to read compressed data from a disk file, decompress the data into a raster image format, and copy the raster image to the display, perhaps re-formatting the pixel data to conform to the display hardware requirements. Some implementations might divide the decompression stage into a stage that does the detailed bit manipulation to decode the video stream and a stage to do image processing, such as inverse discrete cosine transform (IDTC) [KSS96].
Consequences
Benefits
The use of Parallel Pipes and Filters pattern allows the description of a parallel computation in terms of the composition of ordered and simultaneous operations of its component filters. It is a simple solution in which every operation can be understood in terms of input/output relations of ordered data [SG96].
If the computation can be divided into stages with similar amounts of execution time, pipes and filters systems are relatively easy to enhance and maintain by filter exchange and recombination. For parallel systems, reuse is enhanced as filters and pipes are composed as active components. Flexibility is introduced by the addition of new filters, and replacement of old filters by improved ones. As filters and pipes present a simple interface, it is relatively easy to exchange and recombine them within the same architecture [POSA96, SG96].
The performance of pipes and filters architectures depends mostly on the number of steps to be computed. Once all components are active, the processing efficiency is expected to be constant [POSA96, NHST94].
Pipes and filters structures permit certain specialised analysis methods relevant to parallel systems, such as throughput and deadlock analysis [SG96].
Liabilities
The use of pipes and filters introduces potential execution and performance problems if they are not properly load-balanced; this is, if the stages do not all present a similar execution speed. As faster stages will finish processing before slower ones, the parallel system will be as fast as its slowest stage. A common solution to this problem is to execute slow stages on faster processors, but load balancing can still be quite difficult. Another solution is to modify the mapping of software components to hardware processors, and test each stage to get a similar speed. If it is not possible to balance the work load, performance that could potentially be obtained from a pipes and filters system may not be worth the programming effort [Pan96, NHST94].
Synchronisation is another potential problem of pipes and filters systems related with load balance. If each stage causes delay during execution, this delay is spread through all the following filters. Furthermore, if feedback to previous stages is used, there is a potential danger of deadlock [KSS96]which is noticed as the whole system tends to slow down after each operation.
Granularity (the ratio between processing time and communication time) of pipes and filters parallel systems is usually set medium or coarse. This is due to the efficiency of these systems is based on the supposition that pipe communication is a simple action compared to the filters operation. If the time spent communicating tends to be larger than the time required to operate on the flow of data, the performance of the system decreases.
Pipes and Filters systems can degenerate to the point where they become a batch sequential system, this is each step processes all data as a single entity. In this case, each stage does not incrementally process a stream of data. To avoid this situation each filter must be designed to provide a complete incremental parallel transformation of input data to output data [SG96].
The most difficult aspect of pipes and filters systems in general is error handling. An error reporting strategy should at least be defined throughout the system. However, concrete strategies for error recovery or handling depend directly on the problem to solve. Most applications consider that if an error occurs, the system either restarts the pipe, or ignores it. If none of these are possible the use of alternative patterns, such as the Layers pattern [POSA96] is advised.
Related patterns
The Parallel Pipes and Filters pattern for parallel programming is presented as an extension of the original Pipes and Filters pattern [POSA96] and Pipes and Filters architectural style [Shaw95, SG96]. Other patterns that share the similar ordered transformation approach can be found in [PLoP94]; especially consider the Pipe and Filters pattern, the Streams pattern, and the Pipeline pattern [MSM04]. Another pattern that can be consulted for implementation issues using C++ is the Pipeline Design Pattern [VBT95].
3. Summary
The goal of the present work is to provide software designers and engineers with an overview of a common structure used for activity parallel software systems. The architectural pattern described here can be linked with other current pattern developments for concurrent, parallel and distributed systems. Work on patterns that support the design and implementation of such systems has been addressed previously by several authors [Sch95, Sch98a, Sch98b, POSA00].
4. Acknowledgements
The author wishes to thank all those people involved in the improvement of this paper, specially to Doug Lea, my shepherd for EuroPLoP 2005, and Andy Longshaw, who took the time to read and provide insight and useful comments. Also, the author is grateful with the EuroPLoP 2005 attendants of the Writers' Workshop E – Elgar/Enigma, for their comments and suggestions for improvement. This work was developed as part of the Subproject EN101603 of the Support Program to Institutional Projects for Teaching Improvement (PAPIME), supported by DGAPA-UNAM.
5. References
[And00] Gregory R. Andrews. Foundations of Multithreaded, Parallel, and Distributed Programming. Addison-Wesley, 2000.
[CG88] Nicholas Carriero and David Gelernter. How to Write Parallel Programs. A Guide to the Perplexed. Yale University, Department of Computer Science, New Heaven, Connecticut. May 1988.
[CT92] K. Mani Chandy and Stephen Taylor. An Introduction to Parallel Programming. Jones and Bartlett Publishers, Inc., Boston, 1992.
[Fos94] Ian Foster. Designing and Building Parallel Programs, Concepts and Tools for Parallel Software Engineering. Addison-Wesley Publishing Company, 1994.
[GHJV95] Erich Gamma, Richard Helm, Ralph Johnson, and John Vlissides. Design Patterns: Elements of Reusable Object-Oriented Systems. Addison-Wesley, Reading, MA, 1994.
[HPCN98] High Performance Computing and Networking Technology Transfer Nodes. Film, entertainment and video page. ESPRIT project. http://www.hpcn-ttn.org/themegroupsswitch.html. 1998.
[JP96] Jean-Marc Jezequel and Jean-Lin Pacherie. The "Ubiquitous Agent" Design Patterns. Pattern Languages of Programming Conference (PLoP�96). Allerton Park, Illinois, USA, 1996.
[KSS96} Steve Kleiman, Devang Shah, and Bart Smaalders. Programming with Threads. SunSoft Press, Prentice-Hall, 1996.
[LS95] R. Greg Lavender and Douglas C. Schmidt. Active Object. An Object Behavioral Pattern for Concurrent Programming .In Patterns Languages of Programming 2 (PLOP'95). Addison-Wesley, 1996.
[Lea96] Doug Lea. Concurrent Programming in Java. Design, Principles, and Patterns. Addison-Wesley Longman, Inc. Java Series, 1996.
[NHST94] Christopher H. Nevison, Daniel C. Hyde, G. Michael Schneider, Paul T. Tymann. Laboratories for Parallel Computing. Jones and Bartlett Publishers, 1994.
[MSM04] Timothy. G. Mattson, Beverly A. Sanders, and Berna L. Massingill. A Pattern Language for Parallel Programming. Addison Wesley Software Patterns Series, 2004.
[OR98] Jorge L. Ortega-Arjona and Graham Roberts. Architectural Patterns for Parallel Programming. Proceedings of the 3rd European Conference on Pattern Languages of Programming and Computing, EuroPloP'98. Jens Coldewey and Paul Dyson (editors), Universitätsverlag Konstantz GmbH, 1999.
[OR00] Jorge L. Ortega-Arjona. The Communicating Sequential Elements Pattern. Proceedings of the 7th Annual Conference on Pattern Languages of Programming, PloP'98. Eugene Wallingford and Alejandra Garrido (editors), Washigton University Technical Report wucs-00 29, 2000.
[OR03] Jorge L. Ortega-Arjona. The Shared Resource Pattern. Proceedings of the 10th Annual Conference on Pattern Languages of Programming, PloP2003. B. Marrick and M. Schwenk (editors), 2003.
[Pan96] Cherri M. Pancake. Is Parallelism for You? Oregon State University. Originally published in Computational Science and Engineering, Vol. 3, No. 2. Summer, 1996.
[PLoP94] James O. Coplien and Douglas C. Schmidt (editors). Patterns Languages of Programming. Addison-Wesley, 1995.
[PLoP95] James O. Coplien, Norman L. Kerth and John M. Vlissides (editors). Patterns Languages of Programming 2. Addison-Wesley, 1996.
[POSA96] Frank Buschmann, Regine Meunier, Hans Rohnert, Peter Sommerland, Michael Stal. Pattern-Oriented Software Architecture. John Wiley & Sons, Ltd., 1996.
[POSA00] Douglas Schmidt, Michael Stal, Hans Rohnert, Frank Buschmann. Pattern-Oriented Software Architecture, Volume 2. Patterns for Concurrent and Networked Objects. John Wiley & Sons, Ltd., 2000.
[SC95] Aamond Sane and Roy Campbell. Composite Messages: A Structural Pattern for Communication Between Components. OOPSLA'95, Workshop on Design Patterns for Concurrent, Parallel and Distributed Object-Oriented Systems. October 1995.
[Sch95] Douglas Schmidt. Accepted Patterns Papers. OOPSLA'95 Workshop on Design Patterns for Concurrent, Parallel and Distributed Object-Oriented Systems. http://www.cs.wustl.edu/~schmidt/OOPSLA-95/html/papers.html. October, 1995.
[Sch98a] Douglas Schmidt. Design Patterns for Concurrent, Parallel and Distributed Systems. http://www.cs.wustl.edu/~schmidt/patterns-ace.html. January, 1998.
[Sch98b] Douglas Schmidt. Other Pattern URL's. Information on Concurrent, Parallel and Distributed Patterns. http://www.cs.wustl.edu/~schmidt/patterns-info.html. January, 1998.
[Shaw95] Mary Shaw. Patterns for Software Architectures. Carnegie Mellon University. In J. Coplien and D. Schmidt (eds.) Pattern Languages of Program Design. Reading, MA: Addison-Wesley, 1995.
[SG96] Mary Shaw and David Garlan. Software Architecture: Perspectives on an Emerging Discipline. Prentice Hall Publishing, 1996.
[ST96] David B. Skillicorn and Domenico Talia. Models and Languages for Parallel Computation. Computing and Information Science, Queen's University and Universita della Calabria. October 1996.
[VBT95] Allan Vermeulen, Gabe Beged-Dov and Patrick Thompson. The Pipeline Design Pattern. OOPSLA'95, Workshop on Design Patterns for Concurrent, Parallel and Distributed Object-Oriented Systems. October 1995.
[Watt93] Alan Watt. 3D Computer Graphics. Second Edition, Addison-Wesley, 1993.
Copyright 2005 Jorge Luis Ortega-Arjona. Permission is granted to copy for the EuroPLoP 2005 conference. All other rights reserved.
E6-