
Figure 1. An example of a wire divided in n segments with different temperatures.
Abstract
The Communicating Sequential Elements pattern is an architectural pattern for parallel programming, used when a design problem can be understood in terms of domain parallelism. This pattern proposes a solution in which the same operations are performed simultaneously on different pieces of regular data, and operations in each component depend on partial results of neighbour components. Usually, this pattern is presented as a network or logical structure, conceived from the regular data.
1. Introduction
Parallel processing is the division of a problem, presented as a data structure or a set of actions, among multiple processing components that operate simultaneously. The expected result is a more efficient completion of the solution to the problem. The main advantage of parallel processing is its ability to handle tasks of a scale that would be unrealistic or not cost-effective for other systems [CG88, Fos94, ST96, Pan96]. The power of parallelism centres on partitioning a big problem in order to deal with complexity. Partitioning is necessary to divide such a big problem into smaller sub-problems that are more easily understood, and may be worked on separately, on a more "comfortable" level. Partitioning is especially important for parallel processing, because it enables software components to be not only created separately but also executed simultaneously.
Requirements of order of data and operations dictate the way in which a parallel computation has to be performed, and therefore, impact on the software design [OR98]. Depending on how the order of data and operations are present in the problem description, it is possible to consider that most parallel applications fall into one of three forms of parallelism: functional parallelism, domain parallelism, and activity parallelism [OR98]. Examples of each form of parallelism are pipeline processing [VTB95], representing functional parallelism; communicating sequential elements, as an example of domain parallelism; and master-slave [POSA96], which is an instance of activity parallelism.
2. The Communicating Sequential Elements Pattern
The Communicating Sequential Elements pattern is a domain parallelism pattern in which each component performs the same operations on different pieces of regular data. Operations in each component depend on partial results in neighbour components. Usually, this pattern is conceived as a logical structure, reflecting the particular order present in the problem [OR98].
Domain parallelism is the form of parallelism that involves problems in which a set of operations is to be performed on a data structure that exhibits a specific order. Each component in the solution executes a semi-autonomous computation influenced by the computations on its neighbours. The amount of communication between all components can be variable, following fixed and predictable paths that can be represented as a network. In this form of parallelism, it is difficult to conceive the computation as a flow of data among processing stages or sequential steps in an algorithm [CG88, Fos94, OR98, Pan96].
Example: the Heat Equation
Heat is a level of energy present in any physical body, perceptible by its particular temperature. However, even though we can measure an average temperature, in general heat is not evenly distributed throughout all the body. Observing more carefully, it is noticeable that in different parts of the body it is possible to find different temperatures, and hence, different levels of heat. Moreover, these different temperatures vary through time, tending to increase or decrease depending on the interchange of heat between parts of the body. Thus, in a body, different parts expose a different temperature, determining a particular distribution at different times.
In physical and engineering areas, this distribution of heat is particularly important to determine particular thermal properties of materials. The main objective is to obtain a proper representation of the overall effect that allows scientists and engineers to analyse such thermal properties in a more time-efficient way. However, the difficulty of this problem resides in the time to operate on a large number of data pieces and the number of operations per data piece.
For example, let us consider the simplest case, in which the Heat Equation is used to model the heat distribution on a one-dimensional body, a thin substrate, such as a wire, divided in n segments representing different temperatures (Figure 1).

Figure 1. An example of a wire divided in n segments with different temperatures.
The heat diffusion is modelled using a function representing temperature variations depending on time and position in the body. This function is obtained as the solution of a differential equation, known as the Heat Equation [GBDJMS94]. For our example, a function A(t,x) represents the heat diffusion through the wire. A simple method developed for deriving a numerical solution to the Heat Equation is the method of finite differences. The finite differences method cuts the length of the wire into equal parts of length x, and divides the time in discrete segments of length t. Approximating the continuous Heat Equation by its values at the end points of the sub-segments at the discrete time points 0, t, 2t,..., the discrete form for obtaining the heat distribution at the following time step is:
![]()
where i represents time steps, and j represents the position of segments in the wire.
The initial and boundary conditions needed to solve the difference equation numerically are:
![]()
The numerical solution is now computed simply by calculating the value for each segment j at a given time step i, considering the temperature from both its previous and its next segments. The total time required to execute this numerical solution sequentially depends directly on the number of segments and the number of time steps needed to describe the heat distribution through time. The larger number of segments and number of time steps, the longer it takes to compute the solution. A sequential approach that obtains a single temperature value for each segment at each time step is not the most time-efficient way to compute the heat diffusion. However, we can potentially carry out this computation more efficiently by
Using a group of parallel components that exploit a one-dimensional logical structure representing the wire, and
Calculating simultaneously at a given time step the value of A(i+1, j) for all segments.
Context
Start the design of a software program for a parallel system, using a particular programming language for certain parallel hardware. Consider the following context constraints:
The problem involves tasks of a scale that would be unrealistic or not cost-effective for other systems to handle and lends itself to be solved using parallelism. Consider the Heat Equation example: suppose that it is needed to obtain the temperature values for a wire divided into 1,000 segments, considering time steps of 5 milliseconds, during a time frame of 10 seconds. The total number of operations required is 2,000,000.
The hardware platform or machine to be used is given, offering a reasonably good fit to the parallelism found in the problem.
The main objective is to execute the tasks in the most time-efficient way.
Problem
A parallel computation is required that can be performed as a set of operations on regular data. Results cannot be constrained to a one-way flow among processing stages, but each component executes its operations influenced by data values from its neighbouring components. Because of this, components are expected to intermittently exchange data. Communications between components follow fixed and predictable paths.
For instance, consider the Heat Equation example. A one-dimensional body, a wire, can be represented as a data structure, in which the temperature of an segment influences the temperature on adjacent segments and to a different extent, those on either side. Over time, the effects propagate to other segments extending in both directions; even the source segment may experience reverberations due to temperature changes from neighbouring segments. If this example would be executed serially, it would require that the whole computation is performed across every piece of all the data structure to obtain some intermediate state, and then, a new iteration should begin.
Forces
Considering the problem description and granularity and load balance as other elements of parallel design [Fos94, CT92] the following forces should be considered:
The precise order of data distributed among processing elements must be preserved. This order provides the base for result interpretation. For example, in the Heat Equation, it is important to control where and when temperature changes happen, by situating them by segment and time step. This allows obtaining that overall effect expected by scientists and engineers.
Computations must be performed semi-autonomously, on local pieces of data. The objective is to obtain the best possible benefit from domain parallelism. In the Heat Equation example, the wire is divided into segments to operate on them as "autonomous" sub-wires, with similar properties to the original wire, but in a smaller scale.
Every element performs the same operations, in number and complexity. In the Heat Equation example, the same operation must be performed on each segment to obtain its temperature at the next time step. All segments are operated on simultaneously.
Partial results must be communicated among neighbour processing elements. The reason is that operations on each element are influenced by partial results from its neighbouring elements. In the Heat Equation example, it can be noticed that the temperature of an segment at the next time step (A(i+1,j)) results from operating the temperature of the segment at a present time (A(i,j)) with the temperatures from its previous and next segments ( A(i,j-1) and A(i,j+1), respectively).
Improvement in performance is achieved when execution time decreases. Our main objective is to carry out the computation in the most time-efficient way.
Solution
Parallelism is introduced as multiple participating concurrent components, each one applying the same operations on a data subset. Components communicate partial results by exchanging data, usually through communication channels. No data objects are directly shared among components, but each one may access only its own private data subset.
A component communicates by sending data objects from its local space to another. This communication may have different variants: synchronous or asynchronous, exchange of a single data object or a stream of data objects, and one to one, one to many, many to one or many to many communications. Often the data of the problem can be conceived in terms of a regular logical structure. The solution is presented as a network that may reflect this logical structure in a transparent and natural form [CG88, Shaw95, Pan96].
Structure
In this architectural pattern, the same operation is applied in effect simultaneously to different pieces of data. However, operations in each element depend on the partial results of operations in other components. The structure of the solution involves a regular logical structure, conceived from the data structure of the problem. Therefore, the solution is presented as a network of elements that follows the shape imposed by this structure. Identical components simultaneously exist and process during the execution time. Consider our Heat Equation example. An Object Diagram, representing the network of elements that follows the one-dimensional shape of the wire and its division into segments is shown in Figure 2.

Figure 2. Object Diagram of Communicating Sequential Elements for a One-dimensional case.
Participants
Sequential Element. The responsibilities of a processing element are to perform a set of operations on its local data, and to provide a general interface for sending and receiving messages to and from other elements. In the Heat Equation example, identical sequential elements are expected to perform the actual heat calculations and to communicate partial results exchanging values with their neighbours.
Communication Channels. The responsibilities of a communication channel are to represent a medium to send and receive data between elements, and to synchronise communication activity between them. In the Heat Equation problem, channels are expected to handle the communication and synchronisation of temperature values through neighbouring elements.
Dynamics
A typical scenario to describe the basic run-time behaviour of this pattern is presented, where all the Sequential Elements are active at the same time. Every Sequential Element performs the same operations, as a piece of a processing network. In the most simple case (a one-dimensional structure), each one communicates only with a previous and next others (Figure 3). The processing and communicating scenario is as follows:
Initially, all components Element N-1, Element N, Element N+1, etc. read different sub-sets of data. Then, every component communicates its edge data through the available communication channels (Here, Channel A and Channel B). Then all components synchronise and receive the edge data from their previous and next neighbours.
The computation is started when all components Element N-1, Element N, Element N+1, etc. perform Op.1 at the same time.
To continue the computation, all components send their partial results through the available communication channels (Here, Channel A and Channel B). Then all components synchronise again, and receive the partial results from their previous and next neighbours.
Once synchronisation and communications are finished, each component continues computing the next operation (in this case Op.2). The process repeats until each component has finished its computations.
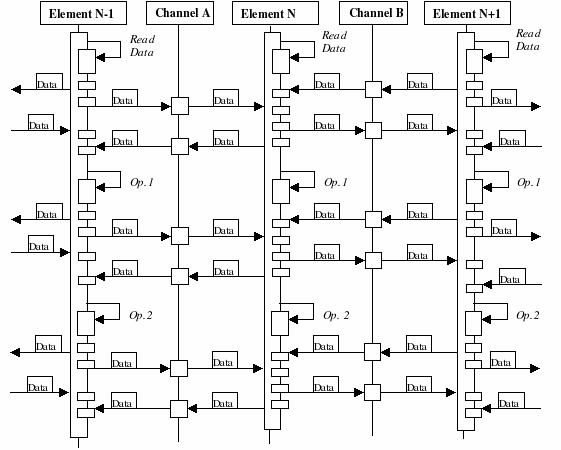
Figure 3. Interaction Diagram of Communicating Sequential Elements for a One-dimensional case.
Implementation
An architectural exploratory approach to design is described below, in which hardware-independent features are considered early, and hardware-specific issues are delayed in the implementation process. This method structures the implementation process of parallel software based on four stages [OR98]. During the first two stages, attention is focused on concurrency and scalability characteristics. In the last two stages, attention is aimed to shift locality and other performance-related issues. Nevertheless, it is preferred to present each stage as general considerations for design instead of providing details about precise implementation. These implementation details are pointed more precisely in the form of references to design patterns for concurrent, parallel, and distributed systems of several other authors [Sch95, Sch98a, Sch98b].
Partitioning. In general, partitioning is concerned with analysing the data structure and algorithm used, searching for a potential parallelism. However, because the Communicating Sequential Elements pattern deals with domain parallelism, the regular logical structure of data is a natural candidate to be straightforward decomposed into a network of data substructures or pieces.
In general, we can initially consider dividing the data structure into a set of data pieces in an arbitrary way, as the regular logical structure is usually considered "homogeneous" (all its parts expose the same properties), and its importance relies only on its order. Thus, data pieces may have different size and shape. However, as we are aiming for an efficient computation, we normally divide the regular data structure into a set of data pieces with similar size and shape. The objective is to load-balance the processing among all the sequential elements.
Trying to expose the maximum concurrency, we define a basic sequential element that processes a unique sequence of operations on its assigned piece of data. We devise this basic sequential element to perform the same operations on different data pieces, so that all sequential elements share the same processing nature and structure. Hence, computations on each sequential element present the same complexity per time step, and the total number of sequential elements is equal to the number of data pieces. Therefore, a sequential element is represented as a single processing element (for instance, a process, task, function, object, etc.) or a subsystem of processing elements, which may be designed using design patterns [GHJV95, POSA96, PLoP94, PLoP95]. Some design patterns that can be considered for implementing sequential elements are the Active Object pattern [LS95], and the "Ubiquitous Agent" pattern [JP96].
Communication. The communication issues are related to the form in which processing components exchange messages. In the particular case of the Communicating Sequential Elements pattern, the sequential elements are connected using communication channels to compose a network that follows the shape of the data structure. Each sequential element is expected to exchange partial results with its neighbours through channels. Thus, channels must perform data exchange and coordinate the operation execution appropriately. An efficient communication depends on the amount and format of the data to be exchanged, and the synchronisation schema used. Both synchronous and asynchronous schemes can be found in several domain parallel systems. However, a synchronous schema is commonly preferred in this pattern because all sequential elements are designed to perform the same operation on the same amount of data during a time step, in a synchronous way.
An important issue to consider here is how communication channels are defined. In general, this decision is linked with the programming language used. Some languages define a type "channel" where it is possible to send and to receive values. Any sequential element is defined to write on the channel, and to read from it. No further implementation is necessary. Conversely, other languages do not define a channel type, or precise ways of data exchange. Thus, we must design and implement channels in such a way that allows data exchange between elements. As the use of channels depends on the language, decisions regarding their implementation can be delayed to other refining design stages.
From an architectural point of view, channels are defined, whether they are implicit in the language, or whether they must be explicitly created. Design patterns that can help with the implementation of channels are the Composite Messages pattern [SC95] and the Service Configurator pattern [JS96].
Agglomeration. The structure of sequential elements and channels defined in previous steps are evaluated with respect to performance. Often, in this kind of structures, agglomeration is directly related with the way data is divided among the sequential elements, this is, the granularity. As each sequential element performs the same operations, changes in the granularity involve only the size of the amount of data pieces in the network to be processed per component. In the case of this pattern, performance is impacted due to redundant communications and the amount of communications in a dimension or direction.
Mapping. Components are assigned to real processors. Mapping can be done statically or dynamically, depending directly on hardware availability and its characteristics.
In the most optimistic case, each sequential element is assigned to a processor. However, the number of processors is usually less than the number of processing elements. Thus, a number of processing elements must be assigned to a processor. To maximise processor utilisation and minimise communication costs, the important feature to consider is load-balance. In domain parallelism, computational efficiency decreases due to load imbalances. If the design is to be used extensively, it is worthwhile to improve its load balance. Approaches include cyclic mapping or dynamic mapping.
As a "rule of thumb", systems based on the Communicating Sequential Elements pattern will perform best on a SIMD (single-instruction, multiple-data) computer, if array operations are available. However, if the computations are relatively independent, a respectable performance can be achieved using a shared-memory system [Pan96]. Further reference about features of parallel hardware platforms and parallel languages can be found in [CSG97, Fos94, Para98, Perr92, Pfis95, Phil95, ST96]. Also, good advice and guidelines about platform and language selection for performance, related with speed-up and scalability, can be found in [Pan96, PB90].
Example Resolved
In this section we continue the Heat Equation example, developing its numerical solution by using a representation of parallel components that reflects the one-dimensional logical structure of the wire, and simultaneously calculating the value of A(i+1,j) for all segments, at a given time frame. The main idea is that data representing the heat in the wire is divided and assigned to a group of communicating elements. In general, elements carry out computations on pieces of data, and channels only allow exchange of data from the boundaries (Figure 4).
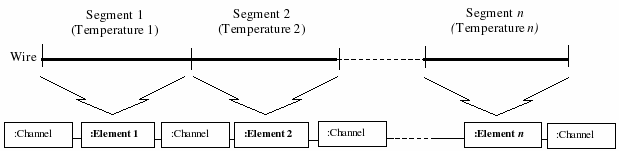
Figure 4. Object Diagram for the Heat Equation Problem, dividing the wire in three segments and assigning them to three sequential elements.
The channels at both extremes just keep track of the values in both extremes, so each communicating element has two channels at both sides.
For this example, we use the UC++ programming language [WRP96] to implement the participant classes. UC++ is an extension of C++ that allows the creation of active objects and different kinds of synchronisation on a PVM environment [GBDJMS94].
Partitioning
The Communicating Sequential Elements pattern is used to obtain a Software Structure that deals with the Heat Equation problem, describing the actual processing as a cooperation between identical sequential elements, which perform calculations and communicate partial results exchanging values through channels with their neighbours. As the actual heat calculations are done in the sequential elements, we present their code first. The prototype of an element for the case study of the Heat Equation is shown in Figure 5.
For this implementation, we take advantage of the characteristics of UC++, making the communicating elements all active objects (as subclass of the class Activatable), aiming to improve performance. We do not show the complete Element() constructor implementation, but essentially, each element copies only its segment of interest into the subwire data structure, determining where on the wire the actual element is operating.
class Element: Activatable {
public:
Element();
Element(Channel* f, Channel* g, int pos, int nElem);
virtual void startWork();
...
private:
int nElements;
int timeStep;
Wire *wire;
Wire *subwire;
Channel *previous;
Channel *next;
...
};
Figure 5. Class Element for the Heat Equation Problem.
Communication
During construction, each element establishes connection with its neighbours through the channels previous and next, which precisely refer to the previous and next sequential element (see Figure 5). All other class attributes represent the parameters required to perform the computation of the Heat Equation.
The function startWork() is called by main()on elements immediately after constructing them. It is here that the parallelism of the algorithm occurs, as this function is executed on each element in parallel, exchanging at each timeStep temperature values representing heat with their neighbours, via the channels previous and next. During this cycle, when all the computations have been carried out, each elements writes a partial result to the wire data structure, repeating until the whole process has covered the time frame of the simulation. It is then when the function printResults() is called, sorting the result and writing it to a file.
Next we present the code for the channel class in Figure 6. This class handles the communication and synchronisation of temperature values through neighbouring elements. The code for the constructor is not shown: it just initialises the buffer values for temporarily store the exchanging values from the previous and next sequential elements. Notice that we again take advantage of the characteristics of UC++, defining the channels also as active objects (a subclass of Activatable). The key functions sendToPrevious(), sendToNext(), receiveFromPrevious() and receiveFromNext() have a similar functionality, retrieving heat values from the sequential elements, and writing them to their neighbours.
class Channel: Activatable {
public:
Channel();
virtual void sendToPrevious(Heat& h);
virtual void sendToNext(Heat& h);
virtual Heat* receiveFromPrevious();
virtual Heat* receiveFromNext();
private:
Heat* first;
Heat* last;
};
Figure 6. Class Channel for the Heat Equation Problem.
Agglomeration and Mapping
Finally, we present the main() function for a Communicating Sequential Elements system in Figure 7. This function initiates and manages the synchronisation of the active objects. Each element is given two pointers of channels to exchange partial results with its neighbours. Active objects are instantiated from the defined classes Element and Channel, by the activenew_Element and activenew_Channel respectively, as defined by UC++. A non-blocking function call to startWork() is then made on each active object, which starts them. Once all elements are active, a blocking function call to blockWait() is done on each of them after the loop for startWork() calls is finished, allowing all elements to complete their computations. The final loop requests to all elements to print their results.
The actual program was developed in UC++ and executed on a PVM environment [GBDJMS94], using a cluster of computers.
int main(int argc, char** argv){
int nElements = 10;
int nChannels = nElements+1;
Channel* channels[nChannels];
Element* elements[nElements];
int i;
for (i = 0; i < nChannels; i++){
channels[i] = activenew_Channel();
}
for (i = 0; i < nElements; i++){
elements[i] = activenew_Element(channels[i],
channels[i+1], i,nElements);
elements[i] -> startWork();
}
for (i = 0; i < nElements; i++){
blockWait(elements[i]);
}
for (i = 0; i < nElements; i++){
elements[i] -> printResults();
}
return 0;
}
Figure 7. main() function for the Heat Equation Problem.
Known uses
Consider as a non-programming example the case of a hive of honey bees. The workers act as constructors, harvesters, soldiers, and nursemaids. Each individual bee can eventually perform any of these activities in cooperation with the others during its short lifetime. Minute-to-minute control of the hive's behaviour is dispersed. Changes, like many shifts in foraging patterns of honey bees come from signals among the workers, whose success or failure at various tasks can rise hive-permeating hormone levels that then brings about changes in the whole hive [OR98].
The one-dimensional wave equation, used to numerical model the motion of vibrating systems, is an example of the Communicating Sequential Elements pattern. The vibrating system is divided in sections, and each processing element is responsible for the computation of the position at any moment of a section. Each computation depends only on partial results of the computation at neighbouring sections. Thus, each computation can be done independently, except when data is required from the previous or next sections [NHST94].
Simulation of dynamic systems, such as an atmosphere model, is another use of Communicating Sequential Elements. The model usually is divided as a rectangular grid of blocks. The simulation proceeds in a series of time steps, where each processing element computes and updates the temporal state in a block with data of the previous state and updates of the state of neighbouring blocks. Integrating the time steps and the blocks makes possible to determine the state of the dynamic system at some future time, based on an initial state [Fos94].
Image processing problems, such as the component labelling problem. An image is given as a matrix of pixels, and each pixel must be labelled according to certain property - for instance, connection. The image is divided in sub-images, and mapped to a network of processing elements. Each processing element tests for connection, and labels all the non-edge pixels of its sub-image. Edge pixels between sub-images are labelled in cooperation by the two respective processing elements [Fos94].
Consequences
Benefits
Data order and integrity is granted because each sequential element accesses only its own local data subset, and there is no data directly shared among components [SG96, ST96].
As all sequential elements share the same functional structure, their behaviour can be modified or changed without excessive effort [SG96, ST96].
It is relatively easy to structure the solution in a transparent and natural form as a network of elements, reflecting the logical structure of data in the problem [CG88, Shaw95, Pan96].
As all components perform the same computation, granularity is independent of functionality, depending only on the size and number of the elements in which data is divided. It is easily to change in case a better resolution or precision is required.
This pattern can be used on most hardware systems, considering the synchronisation between elements as the main restriction (see Liabilities below) [Pan96].
Liabilities
The performance of systems based on communicating elements is significantly impacted by the communication strategy (global or local) used. Usually, the processors available are not enough to support all elements. In order to apply a computation, each processor operates on a subset of the data. Due to this, dependencies between data, expressed as communications, can slow down the program execution [Fos94, Pan96].
Load balancing is a hard problem when using this pattern. Often, data is not easily divided into same-size subsets of data and the computational intensity varies on different processors. To maintain synchronisation means that fast processors must wait until the slow ones can catch up, before the computation can proceed to the next set of operations. An inadequate load balance impacts strongly on performance. The decision to use this pattern should be based on how uniform in almost every aspect the system can be [Pan96].
The synchronous characteristic of the application determines efficiency. If the application is synchronous, a significant amount of effort is required to get a minimal increment in performance. If the application is asynchronous, it is more difficult to parallelise, and probably the effort will not be worthwhile, unless communications between processors are very infrequent [Pan96].
Related patterns
The Communication Sequential Elements pattern is based on the original concept of Communicating Sequential Processes (CSP) [Hoare84]. Patterns that can be considered related to this processing approach are the Ubiquitous Agent Design Pattern [JP96] and the Visibility and Communication between Agents pattern [ABM96].
3. Summary
The goal of the present work is to provide software designers and engineers with an overview of a common structure used for domain parallel software systems. The architectural pattern described here can be linked with other current pattern developments for concurrent, parallel and distributed systems. Work on patterns that support the design and implementation of such systems has been addressed previously by several authors [Sch95, Sch98a, Sch98b].
4. Acknowledgements
I am especially grateful to Douglas C. Schmidt, my shepherd for PLoP 2000, for his comments, suggestions and criticisms to the improvement of this work. This work is part of an ongoing research in the Department of Computer Science, University College London, and funded by the National Autonomous University of Mexico.
5. References
[ABM96] Amund Aarsten, David Brugali and Giuseppe Menga. Patterns for Cooperation. Pattern Languages of Programming Conference (PLoP'96). Allerton Park, Illinois, USA. September 1996.
[CG88] Nicholas Carriero and David Gelernter. How to Write Parallel Programs. A Guide to the Perplexed. Yale University, Department of Computer Science, New Heaven, Connecticut. May 1988.
[CSG97] David Culler, Jaswinder Pal Singh and Anoop Gupta. Parallel Computer Architecture. A Hardware/Software Approach (Preliminary draft). Morgan Kaufmann Publishers, 1997
[CT92] K. Mani Chandy and Stephen Taylor. An Introduction to Parallel Programming. Jones and Bartlett Publishers, Inc., Boston, 1992.
[Fos94] Ian Foster. Designing and Building Parallel Programs, Concepts and Tools for Parallel Software Engineering. Addison-Wesley Publishing Company, 1994.
[GHJV95] Erich Gamma, Richard Helm, Ralph Johnson, and John Vlissides. Design Patterns: Elements of Reusable Object-Oriented Systems. Addison-Wesley, Reading, MA, 1994.
[GBDJMS94] Geist, A., Beguelin, A., Dongarra, J., Jiang, W., Mancheck, R. and Sunderam, V. PVM: Parallel Virtual Machine. A User's Guide and Tutorial for Networked Parallel Computing. The MIT Press, Cambridge, MA, 1994.
[Hoare84] C.A.R. Hoare. Communicating Sequential Processes. Prentice-Hall, 1984.
[JS96] Prashant Jain and Douglas C. Schmidt. Service Configurator. A Pattern for DynamicConfiguration and Reconfiguration of Communication Services. Third Annual Pattern Languages of Programming Conference, Allerton Park, Illinois. September 1996.
[JP96] Jean-Marc Jezequel and Jean-Lin Pacherie. The "Ubiquitous Agent" Design Patterns. Pattern Languages of Programming Conference (PLoP'96). Allerton Park, Illinois, USA, 1996.
[LS95] R. Greg Lavender and Douglas C. Schmidt. Active Object. An Object Behavioral Pattern for Concurrent Programming .In Patterns Languages of Programming 2 (PLOP'95). Addison-Wesley, 1996.
[NHST94] Christopher H. Nevison, Daniel C. Hyde, G. Michael Schneider, Paul T. Tymann. Laboratories for Parallel Computing. Jones and Bartlett Publishers, 1994.
[OR98] Jorge L. Ortega-Arjona and Graham Roberts. Architectural Patterns for Parallel Programming. Proceedings of the 3rd European Conference on Pattern Languages of Programming and Computing, PloP'98. Jens Coldewey and Paul Dyson (editors), Universitätsverlag Konstantz GmbH, 1999.
[Pan96] Cherri M. Pancake. Is Parallelism for You? Oregon State University. Originally published in Computational Science and Engineering, Vol. 3, No. 2. Summer, 1996.
[Para98] David A. Bader. Parascope. A listing of Parallel Computing Sites.
http://computer.org/parascope/index.html . August 1998.
[PB90] Cherri M. Pancake and Donna Bergmark. Do Parallel Languages Respond to the Needs of Scientific Programmers? Computer magazine, IEEE Computer Society. December 1990.
[Perr92] R.H. Perrot. Parallel language developments in Europe: an overview. In Concurrency: Practice and Experience, Vol. 4(8). John Wiley & Sons, Ltd. December 1992.
[Pfis95] Gregory F. Pfister. In Search of Clusters. The Coming Battle in Lowly Parallel Computing. Prentice Hall Inc. 1995.
[Phil95] Michael Philippsen. Imperative Concurrent Object Oriented Languages. Technical report TR-95-050. International Computer Science Institute. Berkeley, California. August 1995.
[PLoP94] James O. Coplien and Douglas C. Schmidt (editors). Patterns Languages of Programming. Addison-Wesley, 1995.
[PLoP95] James O. Coplien, Norman L. Kerth and John M. Vlissides (editors). Patterns Languages of Programming 2. Addison-Wesley, 1996.
[POSA96] Frank Buschmann, Regine Meunier, Hans Rohnert, Peter Sommerland, Michael Stal. Pattern-Oriented Software Architecture. John Wiley & Sons, Ltd., 1996.
[SC95] Aamond Sane and Roy Campbell. Composite Messages: A Structural Pattern for Communication Between Components. OOPSLA'95, Workshop on Design Patterns for Concurrent, Parallel and Distributed Object-Oriented Systems. October 1995.
[Sch95] Douglas Schmidt. Accepted Patterns Papers. OOPSLA'95 Workshop on Design Patterns for Concurrent, Parallel and Distributed Object-Oriented Systems. http://www.cs.wustl.edu/~schmidt/OOPSLA-95/html/papers.html. October, 1995.
[Sch98a] Douglas Schmidt. Design Patterns for Concurrent, Parallel and Distributed Systems. http://www.cs.wustl.edu/~schmidt/patterns-ace.html. January, 1998.
[Sch98b] Douglas Schmidt. Other Pattern URL's. Information on Concurrent, Parallel and Distributed Patterns. http://www.cs.wustl.edu/~schmidt/patterns-info.html. January, 1998.
[Shaw95] Mary Shaw. Patterns for Software Architectures. Carnegie Mellon University. In J. Coplien and D. Schmidt (eds.) Pattern Languages of Program Design. Reading, MA: Addison-Wesley, 1995.
[SG96] Mary Shaw and David Garlan. Software Architecture: Perspectives on an Emerging Discipline. Prentice Hall Publishing, 1996.
[ST96] David B. Skillicorn and Domenico Talia. Models and Languages for Parallel Computation. Computing and Information Science, Queen's University and Universita della Calabria. October 1996.
[VBT95] Allan Vermeulen, Gabe Beged-Dov and Patrick Thompson. The Pipeline Design Pattern. OOPSLA'95, Workshop on Design Patterns for Concurrent, Parallel and Distributed Object-Oriented Systems. October 1995.
[WRP96] Winder, R., Roberts, G., and Poole J. The UC++ project. http://www.dcs.kcl.ac.uk/UC++/