Factorización de Cholesky

Una matriz A simétrica y positiva definida puede ser factorizada de manera eficiente por medio de una matrz triangular infereior y una matriz triangular superior.
Para una matriz no singular la descomposición LU nos lleva a considerar una descomposición de tal tipo A = LU; dadas las condiciones de A, simétrica y definida positiva, no es necesario hacer pivoteo, por lo que ésta factorización se hace eficientemente y en un número de operaciones la mitad de LU tomando la forma  , donde L (la cual podemos "verla" como la raíz cuadrada de A) es una matriz triangular inferior donde los elementos de la diagonal son positivos.

Para resolver un sistema lineal Ax = b con A simétrica definida positiva y dada su factorizaciòn de Cholesky , primero debemos resolver Ly = b y entonces resolver  para lograr x.

Una variante de la factorización de Cholesky es de la forma  , donde R es una matriz triangular superior, en algunas aplicaciones se desea ver la matriz en esa forma y no de otra.

Para encontrar la factorización  , bastaría ver la forma de L y observar las ecuaciones que el producto derecho nos conduce al igualar elementos:

así obtendríamos que:

a₃₂=l₃₁l₂₁+l₃₂l₂₂ l₃₂=(a₃₂-l₃₁l₂₁)/l₂₂, etc. 

y de manera general, para  y :

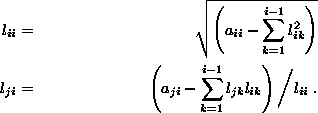
Ahora bien, ya que A es simétrica y definida positiva, podemos asegurar que los elementos sobre la diagonal de L son positivos y los restantes elementos reales desde luego.

Una de las aplicaciones de la factorización de Cholesky es resolver las ecuaciones normales de un problema de cuadrados mínimos, esas ecuaciones son:  , en la que  es simétrica y definida positiva.